1.B. K(G,1) Spaces and Graphs of Groups#
In this section we introduce a class of spaces whose homotopy type depends only on their fundamental group. These spaces arise many places in topology, especially in its interactions with group theory.
A path-connected space whose fundamental group is isomorphic to a given group \(G\) and which has a contractible universal covering space is called a \(\mathbf{K(G,1)\) space. The ‘\(1\)’ here refers to \(\pi_1\). More general \(K(G,n)\) spaces are studied in §4.2. All these spaces are called Eilenberg-MacLane spaces, though in the case \(n=1\) they were studied by Hurewicz before Eilenberg and MacLane took up the general case. Here are some examples:
Example 1B.1. \(S^1\) is a \(K(\mathbb{Z}, 1)\). More generally, a connected graph is a \(K(G,1)\) with \(G\) a free group, since by the results of §1.A its universal cover is a tree, hence contractible.
Example 1B.2. Closed surfaces with infinite \(\pi_1\), in other words, closed surfaces other than \(S^2\) and \(\mathbb{R}P^2\), are \(K(G,1)\)’s. This will be shown in Example 1B.14 below. It also follows from the theorem in surface theory that the only simply-connected surfaces without boundary are \(S^2\) and \(\mathbb{R}^2\), so the universal cover of a closed surface with infinite fundamental group must be \(\mathbb{R}^2\) since it is noncompact. Nonclosed surfaces deformation retract onto graphs, so such surfaces are \(K(G,1)\)’s with \(G\) free.
Example 1B.3. The infinite-dimensional projective space \(\mathbb{R}P^\infty\) is a \(K(\mathbb{Z}_2, 1)\) since its universal cover is \(S^\infty\), which is contractible. To show the latter fact, a homotopy from the identity map of \(S^\infty\) to a constant map be constructed in two stages as follows. First, define \(f_t: \mathbb{R}^\infty \rightarrow \mathbb{R}^\infty\) by \(f_t(x_1,x_2,\cdots) = (1-t)(x_1,x_2,\cdots)+t(0,x_1,x_2,\cdots)\). This takes nonzero vectors to nonzero vectors for all \(t \in [0,1], so f_t / |f_t|\) gives a homotopy from the identity map of \(S^\infty\) to the map \((x_1,x_2,\cdots) \mapsto (0,x_1,x_2,\cdots)\). Then a homotopy from this map to a constant map is given by \(g_t / |g_t|\) where \(g_t(x_1,x_2,\cdots)=(1-t)(0,x_1,x_2,\cdots) +t(1,0,0,\cdots)\).
Example 1B.4. Generalizing the preceding example, we can construct a \(K(\mathbb{Z}_m,1)\) as an infinite-dimensional lens space \(S^\infty / \mathbb{Z}_m\), where \(\mathbb{Z}_m\) acts on \(S^\infty\), regarded as the unit sphere in \(\mathbb{C}^\infty\), by scalar multiplication by \(m^{th}\) roots of unity, a generator of this action being the map \((z_1,z_2,\cdots) \mapsto e^{2\pi i/m}(z_1,z_2,\cdots)\). It is not hard to check that this is a covering space action.
Example 1B.5. A product \(K(G,1) \times K(H,1)\) is a \(K(G \times H,1)\) since its universal cover is the product of the universal covers of \(K(G,1)\) and \(K(H,1)\). By taking products of circles and infinite-dimensional lens spaces we therefore get \(K(G,1)\)’s for arbitrary finitely generated abelian groups \(G\). For example the \(n\)-dimensional torus \(T^n\), the product of \(n\) circles, is a \(K(\mathbb{Z}^n, 1)\).
Example 1B.6. For a closed connected subspace \(K\) of \(S^3\) that is nonempty, the complement \(S^3 - K\) is a \(K(G,1)\). This is a theorem in \(3\)-manifold theory, but in the special case that \(K\) is a torus knot the result follows from our study of torus knot complements in Examples 1.24 and 1.35. Namely, we showed that for \(K\) the torus knot \(K_{m,n}\) there is a deformation retraction of \(S^3-K\) onto a certain \(2\)-dimensional complex \(X_{m,n}\) having contractible universal cover. The homotopy lifting property then implies that the universal cover of \(S^3-K\) is homotopy equivalent to the universal cover of \(X_{m,n}\), hence is also contractible.
Example 1B.7. It is not hard to construct a \(K(G,1)\) for an arbitrary group \(G\), using the notion of a \(\Delta -complex\) defined in §2.1. Let \(EG\) be the \(\Delta\)-complex whose \(n\)-simplices are the ordered \((n+1)\)-tuples \([g_0,\cdots,g_n]\) of elements of \(G\). Such an \(n\)-simplex attaches to the \((n-1)\)-simplices \([g_0,\cdots, \hat{g}_i,\cdots,g_n]\) in the obvious way, just as a standard simplex attaches to its faces. (The notation \(\hat{g}_i\) means that this vertex is deleted.) The complex \(EG\) is contractible by the homotopy \(h_t\) that slides each point \(x \in [g_0, \cdots, g_n]\) along the line segment in \([e,g_0,\cdots,g_n]\) from \(x\) to the vertex \([e]\), where \(e\) is the identity element of \(G\). This is well-defined in \(EG\) since when we restrict to a face \([g_0, \cdots, \hat{g}_i, \cdots, g_n]\) we have the linear deformation to \([e]\) in \([e,g_0,\cdots,\hat{g}_i, \cdots, g_n]\). Note that \(h_t\) carries \([e]\) around the loop \([e,e]\), so \(h_t\) is not actually a deformation retraction of \(EG\) onto \([e]\).
The group \(G\) acts on \(EG\) by left multiplication, an element \(g \in G\) taking the simplex \([g_0,\cdots, g_n]\) linearly onto the simplex \([gg_0, \cdots, gg_n]\). Only the identity \(e\) takes any simplex to itself, so by an exercise at the end of this section, the action of \(G\) on \(EG\) is covering space action. Hence the quotient map \(EG \rightarrow EG/G\) is the universal cover of the orbit space \(BG=EG/G\), and \(BG\) is a \(K(G,1)\).
Since \(G\) acts on \(EG\) by freely permuting simplices, \(BG\) inherits a \(\Delta\)-complex structure from \(EG\). The action of \(G\) on \(EG\) identifies all the vertices of \(EG\), so \(BG\) has just one vertex. To describe the \(\Delta\)-complex structure on \(BG\) explicitly, note first that every \(n\)-simplex of \(EG\) can be written uniquely in the form
The image of this simplex in \(BG\) may be denoted unambiguously by the symbol \([g_1|g_2|\cdots |g_n]\). In this ‘bar’ notation the \(g_i\)’s and their ordered products can be used to label edges, viewing an edge label as the ratio between the two labels on the vertices at the endpoints of the edge, as indicated in the figure. With this notation, the boundary of a simplex \([g_1|\cdots | g_n]\) of \(BG\) consists of the simplices \([g_2|\cdots| g_n],\,[g_1|\cdots|g_{n-1}]\), and \([g_1|\cdots |g_ig_{i+1}|\cdots|g_n]\) for \(i=1,\cdots ,n-1\).
This construction of a \(K(G,1)\) produces a rather large space, since \(BG\) is always infinite-dimensional, and if \(G\) is infinite, \(BG\) has an infinite number of cells in each positive dimension. For example, \(B\mathbb{Z}\) is much bigger than \(S^1\), the most efficient \(K(\mathbb{Z},1)\). On the other hand, \(BG\) has the virtue of being functorial: A homomorphism \(f:G \rightarrow H\) induces a map \(Bf:BG \rightarrow BH\) sending a simplex \([g_1 | \cdots g_n]\) to the simplex \([f(g_1)|\cdots |f(g_n)]\). A different construction of a \(K(G,1)\) is given in §4.2. Here one starts with any \(2\)-dimensional complex having fundamental group \(G\), for example the complex \(X_G\) associated to a presentation of \(G\), and then one attaches cells of dimension \(3\) and higher to make the universal cover contractible without affecting \(\pi_1\). In general, it is hard to get any control on the number of higher-dimensional cells needed in this construction, so it too can be rather inefficient. Indeed, finding an efficient \(K(G,1)\) for a given group \(G\) is often a difficult problem.
It is a curious and almost paradoxical fact that if \(G\) contains any elements of finite order, then every \(K(G,1)\) CW complex must be infinite-dimensional. This is shown in Proposition 2.45. In particular the infinite-dimensional lens space \(K(\mathbb{Z}_m, 1)\)’s in Example 1B.4 cannot be replaced by any finite-dimensional complex.
In spite of the great latitude possible in the construction of \(K(G,1)\)’s, there is a very nice homotopical uniqueness property that accounts for much of the interest in \(K(G,1)\)’s:
Having a unique homotopy type of \(K(G,1)\)’s associated to each group \(G\) means that algebraic invariants of spaces that depend only on homotopy type, such as homology and cohomology groups, become invariants of groups. This has proved to be a quite fruitful idea, and has been much studied both from the algebraic and topological viewpoints. The discussion following Proposition 2.45 gives a few references.
The preceding theorem will follow easily from:
Proposition 1B.9. Let \(X\) be a connected CW complex and let \(Y\) be a \(K(G,1)\). Then every homomorphism \(\pi_1(X,x_0)\rightarrow \pi_1(Y,y_0)\) is induced by a map \((X,x_0) \rightarrow (Y,y_0)\) that is unique up to homotopy fixing \(x_0\).
To deduce the theorem from this, let \(X\) and \(Y\) be CW complex \(K(G,1)\)’s with isomorphic fundamental groups. The proposition gives maps \(f:(X,x_0) \rightarrow (Y,y_0)\) and \(g:(Y,y_0) \rightarrow (X,x_0)\) inducing inverse isomorphisms \(\pi_1(X,x_0) \approx \pi_1(Y,y_0)\). Then \(fg\) and \(gf\) induce the identity on \(\pi_1\) and hence are homotopic to the identity maps.
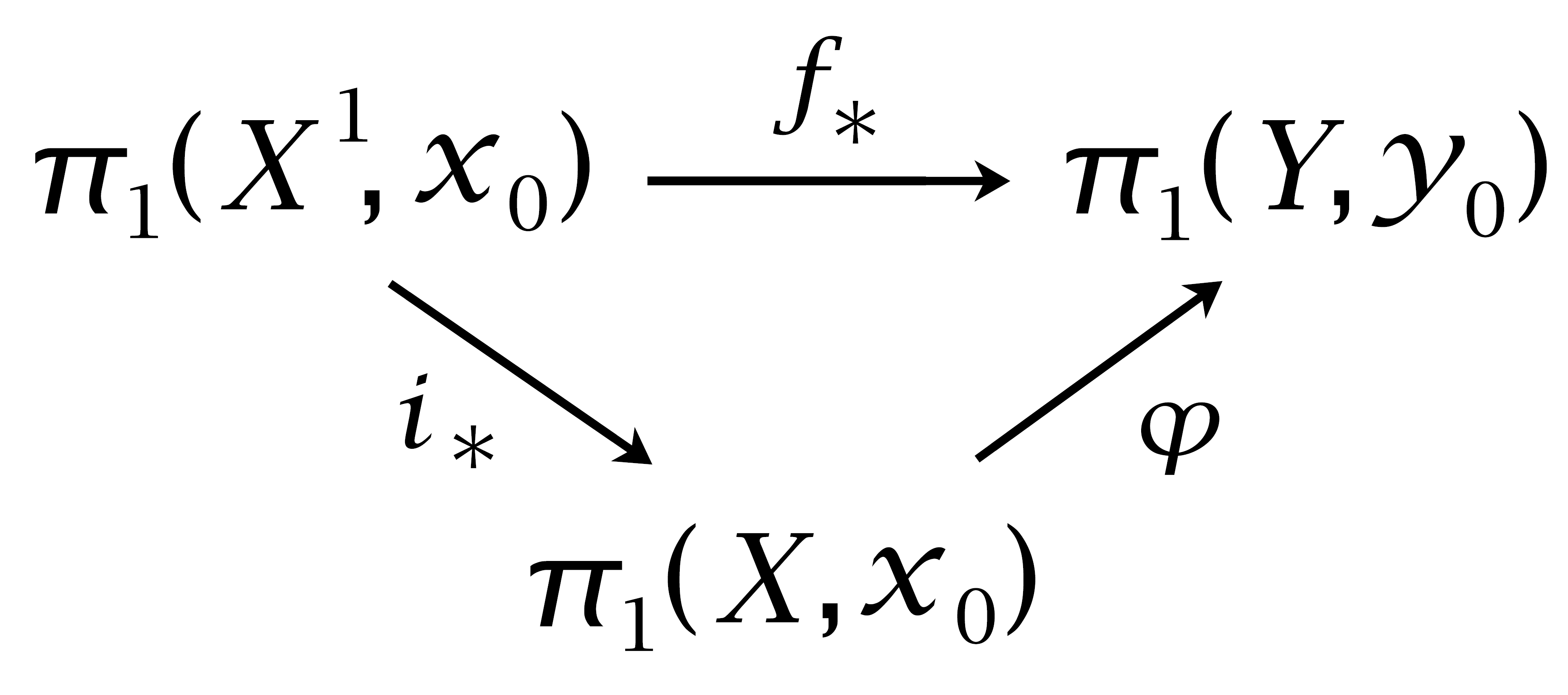
Proof of 1B.9: Let us first consider the case that \(X\) has a single \(0\)-cell, the basepoint \(x_0\). Given a homomorphism \(\varphi: \pi_1(X,x_0) \rightarrow \pi_1(Y,y_0)\), we begin the construction of a map \(f:(X,x_0) \rightarrow (Y,y_0)\) with \(f_* = \varphi\) by setting \(f(x_0)=y_0\). Each \(1\)-cell \(e^1_\alpha\) of \(X\) has closure a circle determining an element \([e^1_\alpha]\in \pi_1(X,x_0)\), and we let \(f\) on the closure of \(e^1_\alpha\) be a map representing \(\varphi([e^1_\alpha])\). If \(i:X^1 \hookrightarrow X\) denotes the inclusion, then \(\varphi i_* = f_*\) since \(\pi_1(X^1,x_0)\) is generated by the elements \([e^1_\alpha]\).
To extend \(f\) over a cell \(e^2_\beta\) with attaching map \(\psi_\beta : S^1 \rightarrow X^1\), all we need is for the composition \(f \psi_\beta\) to be nullhomotopic. Choosing a basepoint \(s_0 \in S^1\) and a path in \(X^1\) from \(\psi_\beta (s_0)\) to \(x_0,\, \psi_\beta\) determines an element \([\psi_\beta] \in \pi_1(X^1, x_0)\), and the existence of a nullhomotopy of \(f\psi_\beta\) is equivalent to \(f_*([\psi_\beta])\) being zero in \(\pi_1(Y,y_0)\). We have \(i_*([\psi_\beta])=0\) since the cell \(e^2_\beta\) provides a nullhomotopy of \(\psi_\beta\) in \(X\). Hence \(f_*([\psi_\beta])=\varphi i_*([\psi_\beta])=0\), and so \(f\) can be extended over \(e^2_\beta\).
Extending \(f\) inductively over cells \(e^n_\gamma\) with \(n>2\) is possible since the attaching maps \(\psi_\gamma : S^{n-1} \rightarrow X^{n-1}\) have nullhomotopic compositions \(f\psi_\gamma : S^{n-1} \rightarrow Y\). This is because \(f\varphi_\gamma\) lifts to the universal cover of \(Y\) if \(n>2\), and this cover is contractible by hypothesis, so the lift of \(f \varphi_\gamma\) is nullhomotopic, hence also \(f\varphi_\gamma\) itself.
Turning to the uniqueness statement, if two maps \(f_0,f_1:(X,x_0) \rightarrow (Y,y_0)\) induce the same homomorphism on \(\pi_1\), then we see immediately that their restrictions to \(X^1\) are homotopic, fixing \(x_0\). To extend the resulting map \(X^1 \times I \cup X \times \partial I \rightarrow Y\) over the remaining cells \(e^n \times (0,1)\) of \(X \times I\) we can proceed just as in the preceding paragraph since these cells have dimension \(n+1 >2\). Thus we obtain a homotopy \(f_t:(X,x_0)\rightarrow (Y,y_0)\), finishing the proof in the case that \(X\) has a single \(0\)-cell.
The case that \(X\) has more than one \(0\)-cell can be treated by a small elaboration on this argument. Choose a maximal tree \(T \subset X\). To construct a map \(f\) realizing a given \(\varphi\), begin by setting \(f(t)=y_0\). Then each edge \(e^1_\alpha\) in \(X-T\) determines an element \([e^1_\alpha] \in \pi_1(X,x_0)\), and we let \(f\) on the closure of \(e^1_\alpha\) be a map representing \(\varphi([e^1_\alpha])\). Extending \(f\) over higher-dimensional cells then proceeds just as before. Constructing a homotopy \(f_t\) joining two given maps \(f_0\) and \(f_1\) with \(f_{0*}=f_{1*}\) also has an extra step. Let \(h_t:X^1 \rightarrow X^1\) be a homotopy starting with \(h_0=\mathbb{1}\) and restricting to a deformation retraction of \(T\) onto \(x_0\). (It is easy to extend such a deformation retraction to a homotopy defined on all of \(X^1\).) We can construct a homotopy from \(f_0 | X^1\) to \(f_1|X^1\) by first deforming \(f_0|X^1\) and \(f_1|X^1\) to take \(T\) to \(y_0\) by composing with \(h_t\), then applying the earlier argument to obtain a homotopy between the modified \(f_0|X^1\) and \(f_1|X^1\). Having a homotopy \(f_0|X^1 \simeq f_1|X^1\) we extend this over all of \(X\) in the same way as before. ◻
The first part of the preceding proof also works for the \(2\)-dimensional complexes \(X_G\) associated to presentations of groups. Thus every homomorphism \(G \rightarrow H\) is realized as the induced homomorphism of some map \(X_G \rightarrow X_H\). However, there is no uniqueness statement for this map, and it can easily happen that different presentations of a group \(G\) give \(X_G\)’s that are not homotopy equivalent.
Graphs of Groups#
As an illustration of how \(K(G,1)\) spaces can be useful in group theory, we shall describe a procedure for assembling a collection of \(K(G,1)\)’s together into a \(K(G,1)\) for a larger group \(G\). Group-theoretically, this gives a method for assembling smaller groups together to form a larger group, generalizing the notion of free products.
Let \(\Gamma\) be a graph that is connected and oriented, that is, its edges are viewed as arrows, each edge having a specified direction. Suppose that at each vertex \(v\) of \(\Gamma\) we place a group \(G_v\) and along each edge \(e\) of \(\Gamma\) we put a homomorphism \(\varphi_e\) from the group at the tail of the edge to the group at the head of the edge. We call this data a graph of groups. Now build a space \(B\Gamma\) by putting the space \(BG_v\) from Example 1B.7 at each vertex \(v\) of \(\Gamma\) and then filling in a mapping cylinder of the map \(B\varphi_e\) along each edge \(e\) of \(\Gamma\), identifying the two ends of the mapping cylinder with the two \(BG_v\)’s at the ends of \(e\). The resulting space \(B\Gamma\) is then a CW complex since the maps \(B\varphi_e\) take \(n\)-cells homeomorphically onto \(n\)-cells. In fact, the cell structure on \(B\Gamma\) can be canonically subdivided into a \(\Delta-complex\) structure using the prism construction from the proof of Theorem 2.10, but we will not need to do this here.
More generally, instead of \(BG_v\) one could take any CW complex \(K(G_v,1)\) at the vertex \(v\), and then along edges put mapping cylinders of maps realizing the homomorphisms \(\varphi_e\). We leave it for the reader to check that the resulting space \(K\Gamma\) is homotopy equivalent to the \(B\Gamma\) constructed above.
Example 1B.10. Suppose \(\Gamma\) consists of one central vertex with a number of edges radiating out from it, and the group \(G_v\) at this central vertex is trivial, hence also all the edge homomorphisms. Then van Kampen’s theorem implies that \(\pi_1(K\Gamma)\) is the free product of the groups at all the outer vertices.
In view of this example, we shall call \(\pi_1(K\Gamma)\) for a general graph of groups \(\Gamma\) the graph product of the vertex groups \(G_v\) with respect to the edge homomorphisms \(\varphi_e\). The name for \(\pi_1(K\Gamma)\) that is generally used in the literature is the rather awkward phrase, ‘the fundamental group of the graph of groups’.
Here is the main result we shall prove about graphs of groups:
Before giving the proof, let us look at some interesting special cases:
Example 1B.12: Free products with Amalgamation. Suppose the graph of groups is \(A \leftarrow C \rightarrow B\), with the two maps monomorphisms. One can regard this data as a specifying embeddings of \(C\) as subgroups of \(A\) and \(B\). Applying van Kampen’s theorem to the decomposition of \(K\Gamma\) into its two mapping cylidners, we see that \(\pi_1(K\Gamma)\) is the quotient of \(A{\Large *}B\) obtained by identifying the subgroup \(C \subset A\) with the subgroup \(C \subset B\). The standard notation for this group is \(A{\Large *}_C B\), the free product of \(A\) and \(B\) amalgamated along the subgroup \(C\). According to the theorem, \(A {\Large *}_C B\) contains both \(A\) and \(B\) as subgroups.
For example, a free product with amalgamation \(\mathbb{Z} {\Large *}_\mathbb{Z} \mathbb{Z}\) can be realized by mapping cylinders of the maps \(S^1 \leftarrow S^1 \rightarrow S^1\) that are \(m\)-sheeted and \(n\)-sheeted covering spaces, respectively. We studied this case in Examples 1.24 and 1.35 where we showed that the complex \(K\Gamma\) is a deformation retract of the complement of a torus knot in \(S^3\) if \(m\) and \(n\) are relatively prime. It is a basic result in \(3\)-manifold theory that the complement of every smooth knot in \(S^3\) can be built up by iterated graph of groups constructions with injective edge homomorphisms, starting with free groups, so the theorem implies that these knot complements are \(K(G,1)\)’s. Their universal covers are all \(\mathbb{R}^3\), in fact.
Example 1B.13: HNN Extensions. Consider a graph of groups \(C \mathrel{\substack {\varphi \\ \longrightarrow\\ \longrightarrow\\ \psi}} A\) with \(\varphi\) and \(\psi\) both monomorphisms. This is analogous to the previous case \(A \leftarrow C \rightarrow B\), but with the two groups \(A\) and :amth:`B` coalesced to a single group. The group \(\pi_1(K\Gamma)\), which was denoted \(A{\large *}_C B\) in the previous case, is now denoted \(A{\large *}_C\). To see what this group looks like, let us regard \(K\Gamma\) as being obtained from \(K(A,1)\) by attaching \(K(C,1) \times I\) along the two ends \(K(C,1)\times \partial I\) via maps realizing the monomorphisms \(\varphi\) and \(\psi\). Using a \(K(C,1)\) with a single \(0\)-cell, we see that \(K\Gamma\) can be obtained from \(K(A,1)\vee S^1\) by attaching cells of dimension two and greatrer, so \(\pi_1(K\Gamma)\) is a quotient of \(A{\large *}\mathbb{Z}\), and it is not hard to figure out that the relations defining this quotient are of the form \(t\varphi (c)t^{-1}=\psi(c)\) where \(t\) is a generator of the \(\mathbb{Z}\) factor and \(c\) ranges over \(C\), or a set of generators for \(C\). We leave the verification of this for the Exercises.
As a very special case, taking \(\varphi=\psi=\mathbb{1}\) gives \(A{\large *}_A=A \times \mathbb{Z}\) since we can take \(K\Gamma = K(A,1) \times S^1\) in this case. More generally, taking \(\varphi = \mathbb{1}\) with \(\psi\) an arbitrary automorphism of \(A\), we realize any semidirect product of \(A\) and \(\mathbb{Z}\) as \(A{\large *}_A\). For example, the Klein bottle occurs this way, with \(\varphi\) realized by the identity map of \(S^1\) and \(\psi\) by a reflection. In this cases when \(\varphi = \mathbb{1}\) we could realize the same group \(\pi_1(K\Gamma)\) using a slightly simpler graph of groups, with a single vertex, labeled \(A\), and a single edge, labeled \(\psi\).
Here is another special case. Suppose we take a torus, delete a small open disk, then identify the resulting boundary circle with a longitudinal circle of the torus. This produces a space \(X\) that happens to be homeomorphic to a subspace of the standard picture of a Klein bottle in \(\mathbb{R}^3\); see Exercise 12 of §1.2. The fundamental group \(\pi_1(X)\) has the form \((\mathbb{Z} * \mathbb{Z})*_\mathbb{Z} \mathbb{Z}\) with the defining relation \(tb^{\pm 1}t^{-1} = aba^{-1}b^{-1}\) where \(a\) is a meridional loop and \(b\) is a longitudinal loop on the torus. The sign of the exponent in the term \(b^{\pm 1}\) is immaterial since the two ways of glueing the boundary circle to the longitude produce homeomorphic spaces. The group \(\pi_1(X)=\langle a,b,t \mid tbt^{-1}aba^{-1}b^{-1} \ranlgle\) abelianizes to \(\mathbb{Z} \times \mathbb{Z}\), but to show that \(\pi_1(X)\) is not isomorphic to \(\mathbb{Z} * \mathbb{Z}\) takes some work. There is a surjection \(\pi_1(X) \rightarrow \mathbb{Z} * \mathbb{Z}\) obtained by setting \(b=1\). This has nontrivial kernel since \(b\) is nontrivial in \(\pi_1(X)\) by the preceding theorem. If \(\pi_1(X)\) were isomorphic to \(\mathbb{Z} \times \mathbb{Z}\), we would then have a surjective homomorphism \(\mathbb{Z} * \mathbb{Z} \rightarrow \mathbb{Z} *\mathbb{Z}\) that was not an isomorphism. However, it is a theorem in group theory that a free group \(F\) is hopfian – every surjective homomorphism \(F \rightarrow F\) must be injective. Hence \(\pi_1(X)\) is not free.
Example 1B.14: Closed Surfaces. A closed orientable surface \(M\) of genus two or greater can be cut along a circle into two compact surfaces \(M_1\) and \(M_2\) such that the closed surfaces obtained from \(M_1\) and \(M_2\) by filling in their boundary circle with a disk have smaller genus than \(M\). Each of \(M_1\) and \(M_2\) is the mapping cylinder of a map from \(S^1\) to a finite graph. Namely, view \(M_i\) as obtained from a closed surface by deleting an open disk in the iterior of the \(2\)-cell in the standard CW structure described in Chapter 0, so that \(M_i\) becomes the mapping cylinder of the attaching map of the \(2\)-cell. This attaching map is not null homotopic, so it induces an injection on \(\pi_1\) since free groups are torsionfree. Thus we have realized the original surface \(M\) as \(K\Gamma\) for \(\Gamma\) a graph of groups of the form \(F_1 \leftarrow \mathbb{Z} \rightarrow F_2\) with \(F_1\) and \(F_2\) free and the two maps injective. The theorem then says that \(M\) is a \(K(G,1)\).
A similar argument works for closed nonorientable surfaces other than \(\mathbb{R}P^2\). For example, the Klein bottle is obtained from two Möbius bands by identifying their boundary circles, and a Möbius band is the mapping cylinder of the \(2\)-sheeted covering space \(S^1 \rightarrow S^1\).
Proof of 1B.11: We shall construct a covering space \(\tilde{K} \rightarrow K \Gamma\) by gluing together copies of the universal covering spaces of the various mapping cylinders in \(K\Gamma\) in such a way that \(\tilde{K}\) will be contractible. Hence \(\tilde{K}\) will be the universal cover of \(K\Gamma\), which will therefore be a \(K(G,1)\).
A preliminary observation: Given a universal covering space \(p:\tilde{X}\rightarrow X\) and a connected, locally path-connected subspace \(A \subset X\) such that the inclusion \(A \hookrightarrow X\) induces an injection on \(\pi_1\), then each component \(\tilde{A}\) of \(p^{-1}(A)\) is a universal cover of \(A\). To see this, note that \(p:\tilde{A} \rightarrow A\) is a covering space, so we have injective maps \(\pi_1(\tilde{A}) \rightarrow \pi_1(A) \rightarrow \pi_1(X)\) whose composition factors through \(\pi_1(\tilde{X})=0\), hence \(\pi_1(\tilde{A})=0\). For example, if \(X\) is the torus \(S^1\times S^1\) and \(A\) is the circle \(S^1 \times \{x_0\}\), then \(p^{-1}(A)\) consists of infinitely many parallel lines in \(\mathbb{R}^2\), each a universal cover of \(A\).
For a map \(f: A\rightarrow B\) between connected CW complexes, let \(p:\tilde{M}_f \rightarrow M_f\) be the universal cover of the mapping cylinder \(M_f\). Then \(\tilde{M}_f\) is itself the mapping cylinder of a map \(\tilde{f}:p^{-1}(A) \rightarrow p^{-1}(B)\) since the line segments in the mapping cylinder structure on \(M_f\) lift to line segments in \(\tilde{M}_f\) defining a mapping cylinder structure. Since \(\tilde{M}_f\) is a mapping cylinder, it deformation retracts onto \(p^{-1}(B)\), so \(p^{-1}(B)\) is also simply-connected, hence is the universal cover of \(B\). If \(f\) induces an injection on \(\pi_1\), then the remarks in the preceding paragraph apply, and the components of \(p^{-1}(A)\) are universal covers of \(A\). If we assume further that \(A\) and \(B\) are \(K(G,1)\)’s, then \(\tilde{M}_f\) and the components of \(p^{-1}(A)\) are contractible, and we claim that \(\tilde{M}_f\) deformation retracts onto each component \(\tilde{A}\) of \(p^{-1}(A)\). Namely, the inclusion \(\tilde{A} \hookrightarrow \tilde{M}_f\) is a homotopy equivalence since both spaces are contractible, and then Corollary 0.20 implies that \(\tilde{M}_f\) deformation retracts onto \(\tilde{A}\) since the pair \((\tilde{M}_f,\tilde{A})\) satisfies the homotopy extension property, as shown in Example 0.15.
Now we can describe the construction of the covering space \(\tilde{K}\) of \(K\Gamma\). It will be the union of an increasing sequence of spaces \(\tilde{K}_1 \subset \tilde{K}_2 \subset \cdots\). For the first stage, let \(\tilde{K}_1\) be the universal cover of one of the mapping cylinders \(M_f\) of \(K\Gamma1\). By the preceding remarks, this contains various disjoint copies of universal covers of the two \(K(G_v,1)\)’s at the ends of \(M_f\). We build \(\tilde{K}_2\) from \(\tilde{K}_1\) by attaching to each of these universal covers of \(K(G_v,1)\)’s a copy of the universal cover of each mapping cylinder \(M_g\) of \(K\Gamma\) meeting \(M_f\) at the end of \(M_f\) in question. Now repeat the process to construct \(\tilde{K}_3\) by attaching universal covers of mapping cylinders at all the universal covers of \(K(G_v,1)\)’s created in the previous step. In the same way, we construct \(\tilde{K}_{n+1}\) from \(\tilde{K}_n\) for all \(n\), and then we set \(\tilde{K}=\bigcup_n \tilde{K}_n\).
Note that \(\tilde{K}_{n+1}\) deformation retracts onto \(\tilde{K}_n\) since it is formed by attaching pieces to \(\tilde{K}_n\) that deformation retract onto the subspaces along which they attach, by our earlier remarks. It follows that \(\tilde{K}\) is contractible since we can deformation retract \(\tilde{K}_{n+1}\) onto \(\tilde{K}_n\) during the time interval \([1/2^{n+1}, 1/2^n]\), and then finish with a contraction of \(\tilde{K}_1\) to a point during the time interval \([\frac{1}{2},1]\).
The natural projection \(\tilde{K} \rightarrow K\Gamma\) is clearly a covering space, so this finishes the proof that \(K\Gamma\) is a \(K(G,1)\).
The remaining statement that each inclusion \(K(G_v,1) \hookrightarrow K\Gamma\) induces an injection on \(\pi_1\) can easily be deduced from the preceding constructuions. For suppose a loop \(\gamma : S^1 \rightarrow K(G_v,1)\) is nullhomotopic in \(K\Gamma\). By the lifting criterion for covering spaces, there is a lift \(\tilde{\gamma}:S^1 \rightarrow \tilde{K}\). This has image contained in one of copies of the universal cover of \(K(G_v,1)\), so \(\tilde{\gamma}\) is nullhomotopic in this universal cover, and hence \(\gamma\) is nullhomotopic in \(K(G_v,1)\). ◻
The various mapping cylinders that make up the universal cover of \(K\Gamma\) are arranged in a treeelike pattern. The tree in question, call it \(T\Gamma\), has one vertex for each copy of a universal cover of a \(K(G_v,1)\) in \(\tilde{K}\), and two vertices are joined by an edge whenever the two universal covers of \(K(G_v,1)\)’s corresponding to these vertices are connected by a line segment lifting a line segment in the mapping cylinder structure of a mapping cylinder of \(K\Gamma\). The inductive construction of \(\tilde{X}\) is reflected in an inductive construction of \(T\Gamma\) as a union of an increasing sequence of subtrees \(T_1 \subset T_2 \subset \cdots\). Corresponding to \(\tilde{K}_1\) is a subtree \(T_1 \subset T\Gamma\) consisting of a central vertex with a number of edges radiating out from it, an ‘asterisk’ with possibly an infinite number of edges. When we enlarge \(\tilde{K}_1\) to \(\tilde{K}_2\), \(T_1\) is correspondingly enlarged to a tree \(T_2\) by attaching a similar asterisk at the end of each outer vertex of \(T_1\), and each subsequent enlargement is handled in the same way. The action of \(\pi_1(K\Gamma)\) on \(\tilde{K}\) as deck transformations induces an action on \(T\Gamma\), permuting its vertices and edges, and the orbit space of \(T\Gamma\) under this action on \(T\Gamma\), permuting its vertices and edges, and the orbit space of \(T\Gamma\) under this action is just the original graph \(\Gamma\). The action on \(T\Gamma\) will not generally be a free action since the elements of a subgroup \(G_v \subset \pi_1(K\Gamma)\) fix the vertex of \(T\Gamma\) corresponding to one of the universal covers of \(K(G_v,1)\).
There is in fact an exact correspondence between graphs of groups and groups acting on trees. See [Scott & Wall 1979] for an exposition of this rather nice theory. From the viewpoint of groups acting on trees, the definition of a graph of groups is usually taken to be slightly more restrictive than the one we have given here, namely, one considers only oriented graphs obtained from an unoriented graph by subdividing each edge by adding a vertex at its midpoint, then orienting the two resulting edges outward, away from the new vertex.
Exercises#
1. Suppose a group \(G\) acts simplicially on a \(\Delta\)-complex \(X\), where ‘simplicially’ means that each element of \(G\) takes each simplex of \(X\) onto another simplex by a linear homeomorphism. If the action is free, show it is a covering space action.
2. Let \(X\) be a connected CW complex and \(G\) a group such that every homomorphism \(\pi_1(X) \rightarrow G\) is trivial. Show that every map \(X \rightarrow K(G,1)\) is nullhomotopic.
3. Show that every graph product of trivial groups is free.
4. Use van Kampen’s theorem to compute \(A{\large *}_C\) as a quotient of \(A{\large *}\mathbb{Z}\), as stated in the text.
5. Consider the graph of groups \(\Gamma\) having one vertex, \(\mathbb{Z}\), and one edge, the map \(\mathbb{Z}\rightarrow \mathbb{Z}\) that is multiplication by \(2\), realized by the \(2\)-sheeted covering spaces \(S^1 \rightarrow S^1\). Show that \(\pi_1(K\Gamma)\) has presentation \(\langle a,b \mid bab^{-1}a^{-2} \rangle\) and describe the universal cover of \(K\Gamma\) explicitly as a product \(T \times \mathbb{R}\) with \(T\) a tree. [The group \(\pi_1(K\Gamma)\) is the first in a family of groups called Baumslag-Solitar groups, having presentations of the form \(\langle a,b \mid ba^mb^{-1}a^{-n}\rangle\). These are HNN extensions \(\mathbb{Z}{\large *}_\mathbb{Z}\).]
6. Show that for a graph of groups all of whose edge homomorphisms are injective maps \(\mathbb{Z} \rightarrow \mathbb{Z}\), we can choose \(K\Gamma\) to have universal cover a product \(T \times \mathbb{R}\) with \(T\) a tree. Work out in detail the case that the graph of groups is the infinite sequence \(\mathbb{Z} \xrightarrow{2} \mathbb{Z} \xrightarrow{3} \mathbb{Z} \xrightarrow{4} \mathbb{Z} \rightarrow \cdots\) where the map \(\mathbb{Z} \rightarrow{n} \mathbb{Z}\) is multiplication by \(n\). Show that \(\pi_1(K\Gamma)\) is isomorphic to \(\mathbb{Q}\) in this case. How would one modify this example to get \(\pi_1(K\Gamma)\) isomorphic to the subgroup of \(\mathbb{Q}\) consisting of rational numbers with denominator of a power of \(2\)?
7. Show that every graph product of groups can be realized by a graph whose vertices are partitioned into two subsets, with every oriented edge going from a vertex in the first subset to a vertex in the second subset.
8. Show that a finite graph product of finitely generated groups is finitely generated, and similarly for finitely presented groups.
9. If \(\Gamma\) is a finite graph of finite groups with injective edge homomorphisms, show that the graph product of the groups has a free subgroup of finite index by constructing a suitable finite-sheeted covering space of \(K\Gamma\) from universal covers of the mapping cylinders in \(K\Gamma\). [The converse is also true: A finitely generated group having a free subgroup of finite index is isomorphic to such a graph product. For a proof of this see [Scott & Wall 1979], Theorem 7.3]