Exercises#
1. Show that composition of paths satisfies the following cancellation property: If \(f_0 \cdot g_0 \simeq f_1 \cdot g_1\) and \(g_0 \simeq g_1\) then \(f_0 \simeq f_1\).
2. Show that the change-of-basepoint homomorphism \(\beta_h\) depends only on the homotopy class of \(h\).
3. For a path-connected space \(X\), show that \(\pi_1 (X)\) is abelian iff all basepoint-change homomorphisms \(\beta_h\) depend only on the endpoints of the path \(h\).
4. A subspace \(X \subset \mathbb{R}^n\) is said to be star-shaped if there is a point \(x_0 \in X\) such that, for each \(x \in X\), the line segment from \(x_0\) to \(x\) lies in \(X\). Show that if a subspace \(X \subset \mathbb{R}^n\) is locally star-shaped, in the sense that every point of \(X\) has a star-shaped neighborhood in \(X\), then every path in \(X\) is homotopic in \(X\) to a piecewise linear path, that is, a path consisting of a finite number of straight line segments traversed at constant speed. Show this applies in particular when \(X\) is open or when \(X\) is a union of finitely many closed convex sets.
5. Show that for a space \(X\), the following three conditions are equivalent:
(a) Every map \(S^1 \rightarrow X\) is homotopic to a constant map, with image a point.
(b) Every map \(S^1 \rightarrow X\) extends to a map \(D^2 \rightarrow X\).
(c) \(\pi_1(X,x_0)=0\) for all \(x_0 \in X\).
Deduce that a space \(X\) is simply-connected iff all maps \(S^1 \rightarrow X\) are homotopic. [In this problem, ‘homotopic’ means ‘homotopic without regard to basepoinbts’.]
6. We can regard \(\pi_1(X,x_0)\) as the set of basepoint-preserving homotopy classes of maps \((S^1,s_0)\rightarrow(X,x_0)\). Let \([S^1, X]\) be the set of homotopy classes of maps \(S^1 \rightarrow X\), with no conditions on basepoints. Thus there is a natural map \(\Phi : \pi_1(X, x_0)\rightarrow [S^1,X]\) obatined by ignoring basepoints. Show that \(\Phi\) is onto if \(X\) is path-connected, and that \(\Phi([f])=\Phi([g])\) iff \([f]\) and \([g]\) are conjugate in \(\pi_1(X,x_0)\). Hence \(\Phi\) induces a one-to-one correspondence between \([S^1, X]\) and the set of conjugacy classes in \(\pi_1(X)\), when \(X\) is path-connected.
7. Define \(f:S^1 \times I \rightarrow S^1 \times I\) by \(f(\theta , s) = (\theta + 2\pi s, s)\), so \(f\) restricts to the identity on the two boundary circles of \(S^1 \times I\). Show that \(f\) is homotopic to the identity by a homotopy \(f_t\) that is stationary on one of the boundary circles, but not by any homotopy \(f_t\) that is stationary on both boundary circles. [Consider what \(f\) does to the path \(s \mapsto (\theta_0 ,s)\) for fixed \(\theta_0 \in S^1\).]
8. Does the Borsuk-Ulam theorem hold for torus? In other words, for every map \(f:S^1 \times S^1 \rightarrow \mathbb{R}^2\) must there exist \((x,y) \in S^1 \times S^1\) such that \(f(x,y) = f(-x,-y)\)?
9. Let \(A_1,\, A_2,\, A_3\) be compact sets in \(\mathbb{R}^3\). Use the Borsuk-Ulam theorme to show that there is one plane \(P \subset \mathbb{R^3}\) that simultaneously divides each \(A_t\) into two pieces of equal measure.
10. From the isomorphism \(\pi_1(X \times Y, (x_0,y_0)) \approx \pi_1(X,x_0) \times \pi_1(Y,y_0)\) it follows that loops in \(X \times \{y_0\}\) and \(\{x_0\}\times Y\) represent commuting elements of \(\pi_1(X \times Y, (x _0, y_0))\). Construct an explicit homotopy demonstrating this.
11. If \(X_0\) is the path-component of a space \(X\) containing the basepoint \(x_0\), show that the inclusion \(X_0 \hookrightarrow X\) induces an isomorphism \(\pi_1(X_0, x_0) \rightarrow \pi_1(X,x_0)\).
12. Show that every homomorphism \(\pi_1(S^1) \rightarrow \pi_1(S^1)\) can be realized as the induced homomorphism \(\varphi_*\) of a map \(\varphi:S^1\rightarrow S^1\).
13. Given a space \(X\) and a path-connected subspace \(A\) containing the basepoint \(x_0\), show that the map \(\pi_1(A,x_0) \rightarrow \pi_1(X, x_0)\) induced by the inclusion \(A \hookrightarrow X\) is surjective iff every path in \(X\) with endpoints in \(A\) is homotopic to a path in \(A\).
14. Show that the isomorphism \(\pi_1(X \times Y) \approx \pi_1(X) \times \pi_1(Y)\) in Proposition 1.12 is given by \([f] \mapsto (p_{1*}([f]), p_{2*}([f]))\) where \(p_1\) and \(p_2\) are the projections of \(X \times Y\) onto its two factors.
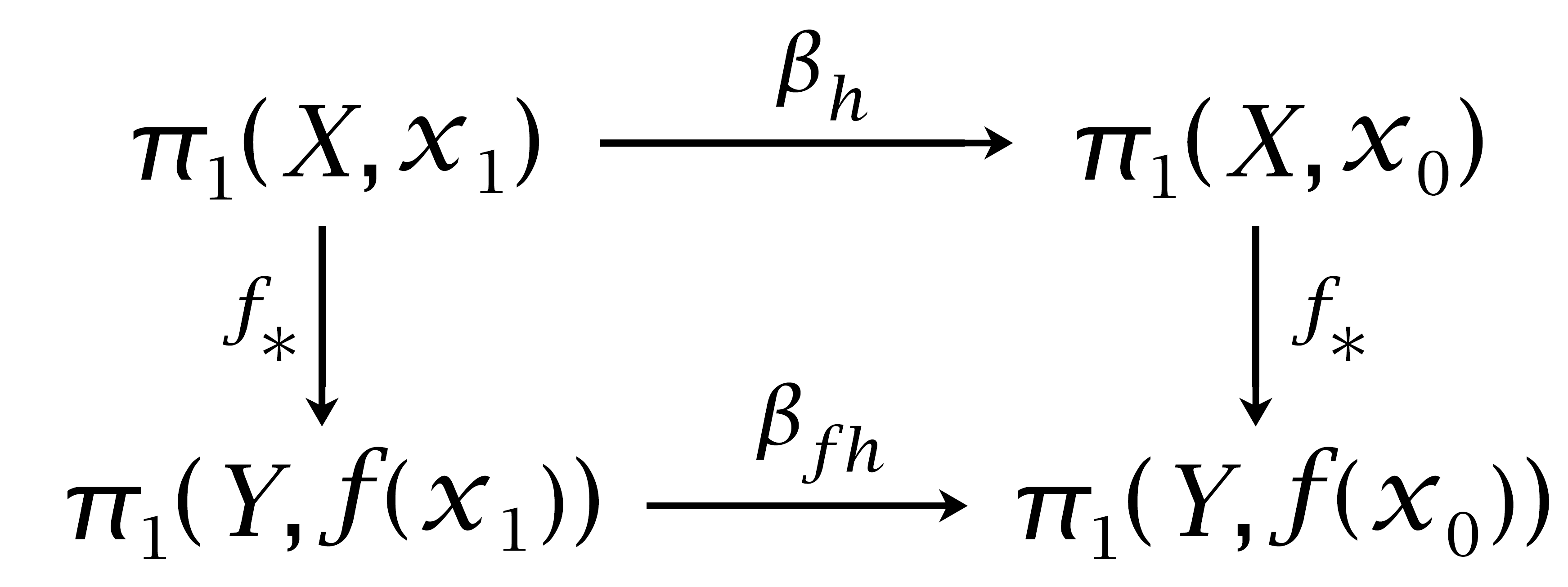
15. Given a map \(f:X \rightarrow Y\) and a path \(h:I \rightarrow X\) from \(x_0\) to \(x_1\), show that \(f_* \beta_h = \beta_{fh} f_*\) in the diagram at the right.
16. Show that there are no retractions \(r: X \rightarrow A\) in the following cases:
(a) \(X=\mathbb{R}^3\) with \(A\) any subspace homeomorphic to \(S^1\).
(b) \(X=S^1 \times D^2\) with \(A\) its boundary torus \(S^1 \times S^1\).
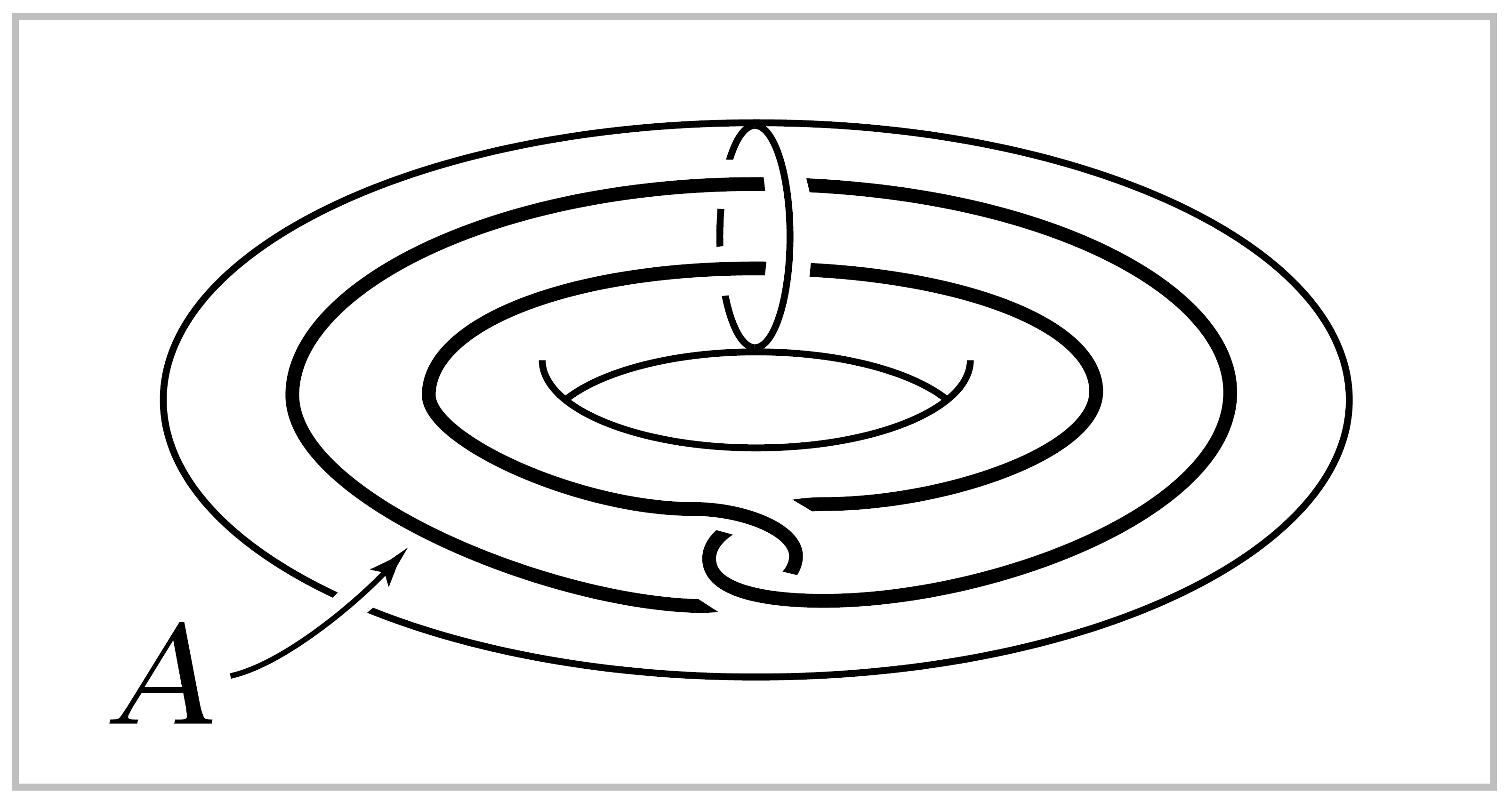
(c) \(X=S^1 \times D^2\) and \(A\) the circle shown in the figure.
(d) \(X=D^2 \vee D^2\) with \(A\) its boundary \(S^1 \vee S^1\).
(e) \(X\) a disk with two points on its boundary identified and \(A\) its boundary \(S^1 \vee S^1\).
(f) \(X\) the Möbius band and \(A\) its boundary circle.
17. Construct infinitely many homotopic retractions \(S^1 \vee S^1 \rightarrow S^1\).
18. Using Lemma 1.15, show that if a space \(X\) is obtinaed from a path-connected subspace \(A\) by attaching a cell \(e^n\) with \(n \geq 2\), then the inclusion \(A \hookrightarrow X\) induces a surjection on \(\pi_1\). Apply this to show:
(a) The wedge sum \(S^1 \vee S^2\) has fundamental group \(\mathbb{Z}\). (b) For a path-connected CW complex \(X\) the inclusion map \(X^1 \hookrightarrow X\) of its \(1\)-skeleton induces a surjection \(\pi_1(X^1) \rightarrow \pi_1(X)\). [For the case that \(X\) has infinitely many cells, see Proposition A.1 in the Appendix.]
19. Show that if \(X\) is a path-connected \(1\)-dimensional CW complex with basepoint \(x_0\) a \(0\)-cell, then every loop in \(X\) is homotopic to a loop consisting of a finite sequence of edges traversed monotonically. [See the proof of Lemma 1.15. This exercise gives an elementary proof that \(\pi_1(S^1)\) is cyclic generated by the standard loop winding once around the circle. The more difficult part of the calculation of \(\pi_1(S^1)\) is therefore the fact that no iterate of this loop is nullhomotopic.]
20. Suppose \(f_t: X \rightarrow X\) is homotopy such that \(f_0\) and \(f_1\) are each the identity map. Use Lemma 1.19 to show that for any \(x_0 \in X\), the loop \(f_t(x_0)\) represents an element of the center of \(\pi_1(X, x_0)\). [One can interpret the result as saying that a loop represents an element of the center of \(\pi_1(X)\) if it extends to a loop of maps \(X \rightarrow X\).]